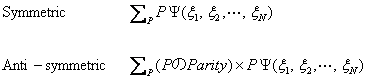２つの粒子を入れ替えた波動関数を想定する。後者の波動関数が物語る物理的な状況は、最初の波動関数のそれとまったく同じでなければならない。その意味は、この状態でのエネルギーその他の物理量を観測しても、最初の波動関数が与えるものと同じにならねばならないということである。このことは、２つの波動関数はたかだか位相因子だけしか違わないということを意味する。なでなら、物理量は波動関数とその共役複素関数との積から計算されるから、波動関数と物理的な状態とは１対１の関係にはなく、位相因子だけの自由度があるからである。第２の波動関数における２つの粒子をもう一度入れ替えると、最初の波動関数からの位相因子の違いはとなるが、これは最初の波動関数と同じものにならねばならない。したがって、となる。すなわち、２つの粒子の交換は、波動関数の符号をそのままにするか、反対にする。このことは、任意の２つの粒子の交換に関して言えることである。

　このことから、一般に、N個量子力学的な同種粒子を記述する波動関数は、その中の任意の２つの粒子の交換に関して、符号をかえないか、符号をかえる。前者の場合を対称Symmetrical, 後者の場合を反対称Antisymmetricalと呼ぶ。さらに、同種粒子がフェルミ粒子である場合は、波動関数は反対称であり、ボース粒子の場合は対称である。このことは複合粒子についても当てはまる。

粒子の互換、置換と波動関数の遇奇性

　長さnのある数列に関して、ある２つの数に注目して、それらを入れ替える操作を互換という。すべての数を対象にした置き換えを置換という。可能な置換の操作はn!である。任意の置換は、互換の組み合わせに分解できる。この時、互換の順序に関係なく、偶数回の互換となるか、奇数回の互換の組み合わせになるかという、「偶奇性」は、置換によって一意的に決まっている。これを置換の偶奇性（Parity）と定義する。数の互換の組み合わせに分解される置換を偶置換と呼び、パリティを＋あるいは１、奇数互換をーあるいはー１に対応させる。

あるN個の変数をもつ波動関数、の全粒子を対象とした置換をPとすれば、対称性および反対称性を備えた新しいN個のための波動関数を以下によって、つくることができる。