[証明]　まず、

　　　　　　　　　

を考える。この関数をを固定してだけを動かしたとして、変化を見る。

　　　　　　　

であるから、なる定義域では(谷状にへこんだ)凹関数concave functionになり、最小値は、なる時で、値はゼロとなる。したがって、

　　　　　　

ここで、と置き、さらに不等式の和をとり、を思い出せば、

　　　　　　　

が得られる。

問題。ギブスの不等式で、と置けば、

　　　　　

エントロピーの上限を与える式がえられる。

フッシャーFisher情報行列

　確率事象の組

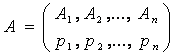
において、確率が個の連続パラベーターに依存しているとする。すなわち、

　　　　　　　　

さらに、これらの各パラメータが微小量だけ違っている分布、